Prediksi Soal UTBK SBMPTN 2020 TPS: Pengetahuan Kuantitatif

Artikel ini memberikan soal prediksi UTBK SBMPTN 2020 untuk TPS (Tes Potensi Skolastik) pengetahuan kuantitatif
—
Para peserta UTBK SBMPTN 2020 akan diukur kemampuan kognitif, logika atau nalar dan pemahaman umum melalui Tes Potensi Skolastik (TPS). Materi TPS UTBK menghadirkan beberapa tipe soal yaitu penalaran umum, pemahaman bacaan, pengetahuan umum, dan pengetahuan kuantitatif. Agar kamu lebih siap, yuk kita berlatih menggunakan prediksi soal TPS pengetahuan kuantitatif berikut ini.
Baca juga: Latihan Soal UTBK SBMPTN 2019 TPS

Subtopik : Bilangan
1. Jika ![]() adalah pembulatan bilangan
adalah pembulatan bilangan![]() ke satuan terdekat, maka nilai
ke satuan terdekat, maka nilai 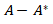 untuk
untuk 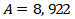 adalah ….
adalah ….

JAWABAN : D
PEMBAHASAN :
Karena 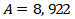 ; maka akan didapat
; maka akan didapat ![]() . Sehingga
. Sehingga
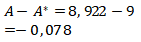

Subtopik : Bilangan
2. Nilai dari  adalah ….
adalah ….
- 4.000
- 8.500
- 10.000
- 12.500
- 20.000
JAWABAN : C
PEMBAHASAN :
Perhatikan bahwa
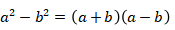
Sehingga
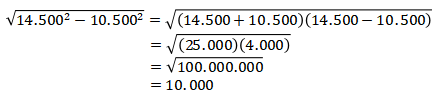

Subtopik : Bilangan, Aljabar
3. Dalam ruang kelas, diketahui ![]() siswa adalah perempuan. Jika sebanyak
siswa adalah perempuan. Jika sebanyak ![]() dari siswa perempuan dan
dari siswa perempuan dan ![]() dari siswa laki-laki suka menggambar, maka banyaknya siswa yang tidak suka menggambar adalah … dari seluruh siswa.
dari siswa laki-laki suka menggambar, maka banyaknya siswa yang tidak suka menggambar adalah … dari seluruh siswa.
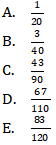
JAWABAN : E
PEMBAHASAN :
Banyak siswa perempuan = ![]() dari seluruh siswa.
dari seluruh siswa.
Banyak siswa laki-laki = 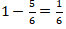 dari seluruh siswa.
dari seluruh siswa.
Banyak siswa perempuan yang suka menggambar =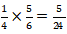
Banyak siswa laki-laki yang suka menggambar =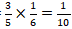
Banyak keseluruhan siswa yang suka menggambar = 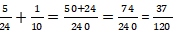
Sehingga banyak siswa yang tidak suka menggambar adalah 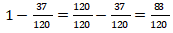 dari seluruh siswa.
dari seluruh siswa.

Subtopik : Bilangan, Aljabar
4. Suatu bilangan memiliki nilai yang sama dengan pecahan ![]() . Jika pembilangnya dikurang 3 dan penyebutnya dikurang 8, maka didapatkan bilangan yang senilai dengan pecahan
. Jika pembilangnya dikurang 3 dan penyebutnya dikurang 8, maka didapatkan bilangan yang senilai dengan pecahan ![]() Jika pembilangnya ditambah 3 dan penyebutnya dikurang 2, maka didapatkan bilangan yang senilai dengan pecahan ….
Jika pembilangnya ditambah 3 dan penyebutnya dikurang 2, maka didapatkan bilangan yang senilai dengan pecahan ….
![]()
JAWABAN : A
PEMBAHASAN :
Misalkan pecahan yang dimaksud adalah ![]() .
.
Pecahan tersebut memiliki nilai yang sama dengan pecahan ![]() maka
maka
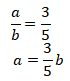
Jika pembilangnya dikurang 3 dan penyebutnya dikurang 8, maka didapatkan bilangan yang senilai dengan pecahan ![]() Sehingga
Sehingga
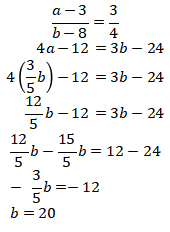
Maka
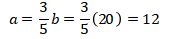
Sehingga jika pembilangnya ditambah 3 dan penyebutnya dikurang 2, maka
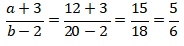

Subtopik : Aljabar
5. Diketahui 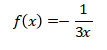 untuk setiap bilangan real tak nol. Jika
untuk setiap bilangan real tak nol. Jika 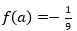 dan
dan 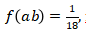 , maka
, maka 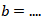
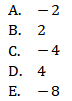
JAWABAN : A
PEMBAHASAN :
Perhatikan bahwa
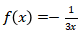
Sehingga
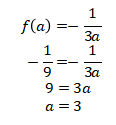
Dan
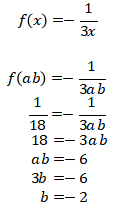

Subtopik : Geometri
6. Mana titik yang terletak pada kurva 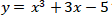 ?
?
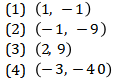
- (1), (2), dan (3) SAJA yang benar.
- (1) dan (3) SAJA yang benar.
- (2) dan (4) SAJA yang benar.
- HANYA (4) yang benar
- SEMUA pilihan benar.
JAWABAN : A
PEMBAHASAN :
(1) 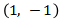
Jika ![]() , maka
, maka
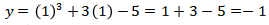
Maka didapat titik 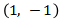 terletak pada kurva.
terletak pada kurva.
(2) 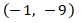
Jika 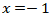 , maka
, maka
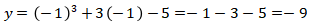
Maka didapat titik 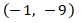 terletak pada kurva.
terletak pada kurva.
(3) ![]()
Jika ![]() , maka
, maka
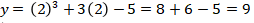
Maka didapat titik ![]() terletak pada kurva.
terletak pada kurva.
(4) 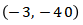
Jika 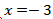 , maka
, maka
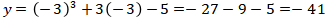
Maka didapat titik 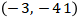 terletak pada kurva.
terletak pada kurva.
Maka titik-titik yang terletak pada kurva ditunjukkan oleh nomor (1), (2), dan (3).

Subtopik : Geometri
7. Manakah di antara sifat-sifat berikut yang merupakan sifat belah ketupat?
(1) Sudut-sudut yang berhadapan sama besar
(2) Setiap sisinya memiliki panjang yang berbeda
(3) Kedua diagonalnya saling tegak lurus
(4) Kedua diagonalnya sama panjang
- (1), (2), dan (3) SAJA yang benar.
- (1) dan (3) SAJA yang benar.
- (2) dan (4) SAJA yang benar.
- HANYA (4) yang benar
- SEMUA pilihan benar.
JAWABAN : B
PEMBAHASAN :
Perhatikan gambar belah ketupat berikut :
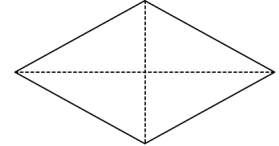
Beberapa sifat dari belah ketupat adalah
(1) Sudut-sudut yang berhadapan sama besar
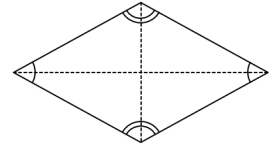
(2) Semua sisinya sama panjang
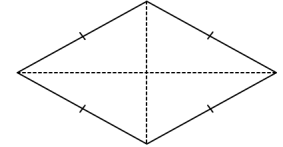
(3) Kedua diagonalnya saling tegak lurus
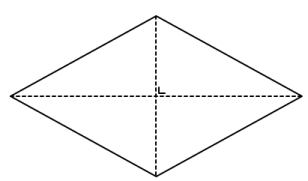
(4) Kedua diagonalnya TIDAK sama panjang, NAMUN perpotongan diagonalnya memotong kedua diagonal menjadi dua bagian yang sama panjang
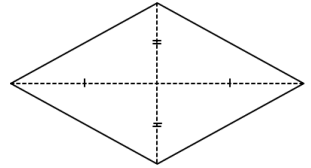
Sehingga pernyataan yang tepat adalah pernyataan (1) dan (3).

Subtopik : Peluang
8. Dalam sebuah kotak terdapat 4 bola merah, 5 bola kuning, 8 bola hijau, dan 3 bola biru. Jika diambil satu bola dari dalam kotak, manakah pernyataan yang benar?
(1) Peluang terambilnya bola merah adalah ![]()
(2) Peluang terambilnya bola bukan kuning adalah ![]()
(3) Peluang terambilnya bola hijau adalah ![]()
(4) Peluang terambilnya bola bukan biru adalah ![]()
- (1), (2), dan (3) SAJA yang benar.
- (1) dan (3) SAJA yang benar.
- (2) dan (4) SAJA yang benar.
- HANYA (4) yang benar
- SEMUA pilihan benar.
JAWABAN : E
PEMBAHASAN :
Banyak bola secara keseluruhan adalah 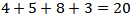 bola.
bola.
(1) Peluang terambilnya bola merah adalah ![]()
Banyak bola merah = 4. Maka peluang terambilnya bola merah adalah 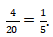
(2) Peluang terambilnya bola bukan kuning adalah ![]()
Banyak bola bukan kuning = 4 + 8 + 3 = 15. Maka peluang terambilnya bola bukan kuning adalah 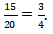
(3) Peluang terambilnya bola hijau adalah ![]()
Banyak bola hijau = 8. Maka peluang terambilnya bola hijau adalah 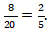
(4) Peluang terambilnya bola bukan biru adalah ![]()
Banyak bola bukan biru = 4 + 5 + 8 = 17. Maka peluang terambilnya bola bukan biru adalah ![]()
Maka semua pernyataan benar.

Subtopik : Aljabar
9. Jika diketahui sistem persamaan linear dua variabel sebagai berikut
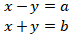
Mana nilai a dan b sedemikian sehingga didapat penyelesaian x dan y yang merupakan bilangan bulat?
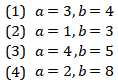
- (1), (2), dan (3) SAJA yang benar.
- (1) dan (3) SAJA yang benar.
- (2) dan (4) SAJA yang benar.
- HANYA (4) yang benar
- SEMUA pilihan benar.
JAWABAN : C
PEMBAHASAN :
Perhatikan sistem persamaan linear dua variabel sebagai berikut
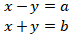
Jika kedua persamaan tersebut dijumlahkan, maka didapat
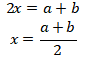
Substitusikan ke persamaan kedua
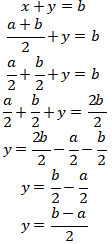
Sehingga didapat 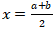 dan
dan 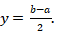 .
.
(1) 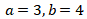
Didapat
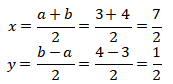
Didapat x dan y yang bukan merupakan bilangan bulat. (PERNYATAAN SALAH)
(2) 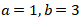
Didapat
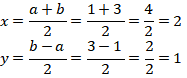
Didapat x dan y yang merupakan bilangan bulat. (PERNYATAAN BENAR)
(3)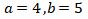
Didapat
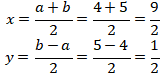
Didapat x dan y yang bukan merupakan bilangan bulat. (PERNYATAAN SALAH)
(4)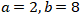
Didapat
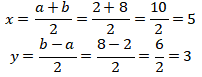
Didapat x dan y yang merupakan bilangan bulat. (PERNYATAAN BENAR)
Maka nilai a dan b sedemikian sehingga didapat penyelesaian x dan y yang merupakan bilangan bulat hanya ditunjukkan oleh nomor (2) dan (4).

Subtopik : Bilangan
10. Manakah waktu yang setara dengan lebih dari 3.000 tahun?
(1) 39.999 bulan
(2) 599 lustrum
(3) 399 dasawarsa
(4) 299 windu
- (1), (2), dan (3) SAJA yang benar.
- (1) dan (3) SAJA yang benar.
- (2) dan (4) SAJA yang benar.
- HANYA (4) yang benar
- SEMUA pilihan benar.
JAWABAN : B
PEMBAHASAN :
(1) 39.999 bulan
Ingat bahwa 12 bulan = 1 tahun atau 1 bulan = ![]() tahun. Maka
tahun. Maka

Sehingga lebih dari 3.000 tahun.
(2) 599 lustrum
Ingat bahwa 1 lustrum = 5 tahun. Maka
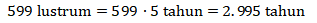
Sehingga kurang dari 3.000 tahun.
(3) 399 dasawarsa
Ingat bahwa 1 dasawarsa = 10 tahun. Maka
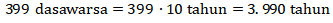
Sehingga lebih dari 3.000 tahun.
(4) 299 windu
Ingat bahwa 1 windu = 8 tahun. Maka
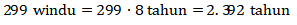
Sehingga kurang dari 3.000 tahun.
Maka waktu yang setara dengan lebih dari 3.000 tahun ditunjukkan oleh nomor (1) dan (3).

Subtopik : Aljabar
11. Diketahui beberapa kamar di hotel Aakan ditempati oleh atlet-atlet olimpiade. Berapa banyak atlet yang akan menginap?
(1) Jika satu kamar diisi oleh 7 orang atlet, maka terdapat 1 kamar yang tidak terisi.
(2) Jika satu kamar diisi oleh 6 orang atlet, maka terdapat 14 orang atlet yang tidak mendapatkan kamar.
- Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup.
- Pernyataan (2) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (1) SAJA tidak cukup.
- DUA pernyataan BERSAMA-SAMA cukup untuk menjawab pertanyaan, tetapi SATU pernyataan SAJA tidak cukup.
- Pernyataan (1) SAJA cukup untuk menjawab pertanyaan dan pernyataan (2) SAJA cukup.
- Pernyataan (1) dan pernyataan (2) tidak cukup untuk menjawab pertanyaan.
JAWABAN : C
PEMBAHASAN :
Misalkan banyaknya kamar adalah x dan banyaknya atlet adalah y.
Pernyataan (1)
Jika satu kamar diisi oleh 7 orang atlet, maka terdapat 1 kamar yang tidak terisi.
Terdapat 1 kamar yang tidak terisi, sehingga banyak kamar yang digunakan adalah x – 1 kamar.
Karena setiap kamar diisi oleh 7 orang atlet, maka banyaknya atlet secara keseluruhan adalah
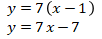
Perhatikan bahwa banyaknya atlet masih bergantung dengan banyaknya kamar. Sehingga belum terjawab berapa banyak atlet yang akan menginap.
Pernyataan (2)
Jika satu kamar diisi oleh 6 orang atlet, maka terdapat 14 orang atlet yang tidak mendapatkan kamar.
Satu kamar diisi oleh 6 orang atlet, maka banyak atlet yang sudah menempati kamar adalah 6x.
Tetapi, terdapat 14 orang atlet yang tidak mendapat kamar. Sehingga banyak atlet secara keseluruhan adalah
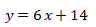
Perhatikan bahwa banyaknya atlet masih bergantung dengan banyaknya kamar. Sehingga belum terjawab berapa banyak atlet yang akan menginap.
Sehingga masing-masing pernyataan tidaklah cukup untuk menjawab pertanyaan. Maka cek gabungan kedua pernyataan.
Gabungan pernyataan (1) dan (2)
Jika satu kamar diisi oleh 7 orang atlet, maka terdapat 1 kamar yang tidak terisi dan jika satu kamar diisi oleh 6 orang atlet, maka terdapat 14 orang atlet yang tidak mendapatkan kamar.
Dari kedua pernyataan didapat dua buah persamaan, yaitu
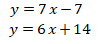
Sehingga
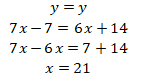
Maka
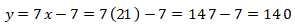
Sehingga terjawab bahwa terdapat 140 atlet yang akan menginap.
Maka, DUA pernyataan BERSAMA-SAMA cukup untuk menjawab pertanyaan, tetapi SATU pernyataan SAJA tidak cukup.

Subtopik : Geometri
12. Berapakah luas dari lingkaran B?
(1) Lingkaran B memiliki jari-jari 5 cm.
(2) Keliling dari lingkaran B adalah ![]() cm.
cm.
- Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup.
- Pernyataan (2) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (1) SAJA tidak cukup.
- DUA pernyataan BERSAMA-SAMA cukup untuk menjawab pertanyaan, tetapi SATU pernyataan SAJA tidak cukup.
- Pernyataan (1) SAJA cukup untuk menjawab pertanyaan dan pernyataan (2) SAJA cukup.
- Pernyataan (1) dan pernyataan (2) tidak cukup untuk menjawab pertanyaan.
JAWABAN : D
PEMBAHASAN :
Pernyataan (1)
Lingkaran B memiliki jari-jari 5 cm.
Karena 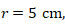 maka
maka
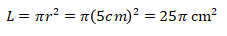
Sehingga luas lingkaran dapat dicari.
Pernyataan (2)
Keliling dari lingkaran B adalah ![]() cm.
cm.
Karena 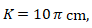 maka
maka
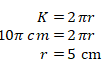
Sehingga
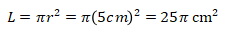
Sehingga luas lingkaran dapat dicari.
Maka, pernyataan (1) SAJA cukup untuk menjawab pertanyaan dan pernyataan (2) SAJA cukup.

Subtopik : Bilangan
13. Sebanyak 20 jeruk di kotak P, masing-masing memiliki berat yang kurang dari setiap jeruk yang ada di kotak Q. Jika di kotak Q terdapat 19 jeruk, berapakah median berat dari 39 jeruk di kotak P dan Q?
(1) Berat dari jeruk yang paling ringan di kotak Q adalah 90 gram.
(2) Berat dari jeruk yang paling berat di kotak P adalah 75 gram.
- Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup.
- Pernyataan (2) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (1) SAJA tidak cukup.
- DUA pernyataan BERSAMA-SAMA cukup untuk menjawab pertanyaan, tetapi SATU pernyataan SAJA tidak cukup.
- Pernyataan (1) SAJA cukup untuk menjawab pertanyaan dan pernyataan (2) SAJA cukup.
- Pernyataan (1) dan pernyataan (2) tidak cukup untuk menjawab pertanyaan.
JAWABAN : B
PEMBAHASAN :
Misalkan berat jeruk-jeruk tersebut setelah diurutkan dari yang paling ringan hingga paling berat adalah 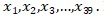 Maka jeruk-jeruk dengan berat
Maka jeruk-jeruk dengan berat 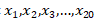 berada di kotak P dan jeruk-jeruk dengan berat
berada di kotak P dan jeruk-jeruk dengan berat 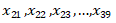 berada di kotak Q.
berada di kotak Q.
Median berat dari 39 jeruk tersebut adalah ![]() , yang berarti berat jeruk yang paling berat di kotak P.
, yang berarti berat jeruk yang paling berat di kotak P.
Pernyataan (1)
Berat dari jeruk yang paling ringan di kotak Q adalah 90 gram.
Dari pernyataan ini dapat diketahui 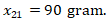
Namun tidak diketahui dengan pasti nilai dari ![]() .
.
Sehingga belum terjawab berapa median berat dari 39 jeruk tersebut.
Pernyataan (2)
Berat dari jeruk yang paling berat di kotak P adalah 75 gram.
Dari pernyataan ini dapat diketahui 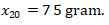
Sehingga terjawab bahwa median berat jeruk adalah 75 gram.
Maka, pernyataan (2) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (1) SAJA tidak cukup.

Subtopik : Aljabar
14. Jika 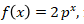 , maka berapakah nilai dari
, maka berapakah nilai dari ![]() ?
?
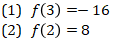
- Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup.
- Pernyataan (2) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (1) SAJA tidak cukup.
- DUA pernyataan BERSAMA-SAMA cukup untuk menjawab pertanyaan, tetapi SATU pernyataan SAJA tidak cukup.
- Pernyataan (1) SAJA cukup untuk menjawab pertanyaan dan pernyataan (2) SAJA cukup.
- Pernyataan (1) dan pernyataan (2) tidak cukup untuk menjawab pertanyaan.
JAWABAN : A
PEMBAHASAN :
Perhatikan bahwa
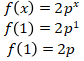
Pernyataan (1)
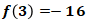
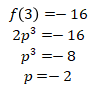
Maka
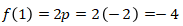
Sehingga terjawab bahwa 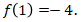 .
.
Pernyataan (2)
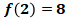
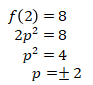
Maka
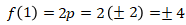
Sehingga belum terjawab berapa nilai dari ![]() karena terdapat dua nilai yang memenuhi.
karena terdapat dua nilai yang memenuhi.
Maka, pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup.

Subtopik : Aljabar
15. Apakah ![]() ?
?
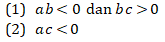
- Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup.
- Pernyataan (2) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (1) SAJA tidak cukup.
- DUA pernyataan BERSAMA-SAMA cukup untuk menjawab pertanyaan, tetapi SATU pernyataan SAJA tidak cukup.
- Pernyataan (1) SAJA cukup untuk menjawab pertanyaan dan pernyataan (2) SAJA cukup.
- Pernyataan (1) dan pernyataan (2) tidak cukup untuk menjawab pertanyaan.
JAWABAN : E
PEMBAHASAN :
Pernyataan (1)

Pernyataan (2)

Sehingga masing-masing pernyataan tidaklah cukup. Maka cek gabungan kedua pernyataan.
Gabungan pernyataan (1) dan (2)
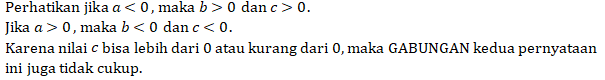
Maka, Pernyataan (1) dan pernyataan (2) tidak cukup untuk menjawab pertanyaan.

Subtopik : Peluang
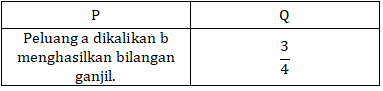
16. Jika ![]() adalah bilangan yang dipilih dari himpunan {1, 2, 3, 4, 5} dan b adalah bilangan yang dipilih dari himpunan {6, 7, 8, 9}.
adalah bilangan yang dipilih dari himpunan {1, 2, 3, 4, 5} dan b adalah bilangan yang dipilih dari himpunan {6, 7, 8, 9}.
Manakah hubungan yang benar antara kuantitas P dan Q berikut berdasarkan informasi yang diberikan?
- P > Q
- Q > P
- P = Q
- Informasi yang diberikan tidak cukup untuk memutuskan salah satu dari tiga pilihan di atas.
JAWABAN : B
PEMBAHASAN :
Supaya ![]() ganjil, maka
ganjil, maka ![]() harus ganjil dan b juga harus ganjil. Perhatikan bahwa pemilihan bilangan
harus ganjil dan b juga harus ganjil. Perhatikan bahwa pemilihan bilangan ![]() tidak akan memengaruhi pemilihan bilangan b, maka
tidak akan memengaruhi pemilihan bilangan b, maka
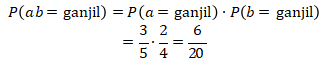
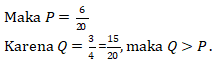

Subtopik : Peluang
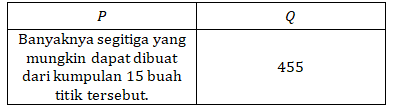
17. Terdapat 15 buah titik yang tidak saling segaris.
Manakah hubungan yang benar antara kuantitas P dan Q berikut berdasarkan informasi yang diberikan?
- P > Q
- Q > P
- P = Q
- Informasi yang diberikan tidak cukup untuk memutuskan salah satu dari tiga pilihan di atas.
JAWABAN : C
PEMBAHASAN :
Untuk membuat segitiga, dibutuhkan tiga buah titik.
Sehingga mencari banyaknya segitiga yang mungkin dapat dibuat sama halnya dengan mencari banyaknya cara memilih 3 dari 15 titik yang tersedia. Sehingga didapat banyaknya segitiga adalah
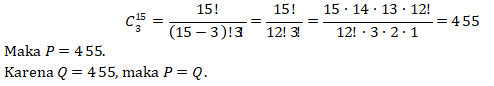

Subtopik : Bilangan
18. Pak Rohmat membeli 5 lusin donat seharga Rp66.000/lusin dan 3 lusin donat seharga Rp5.500/donat.
Manakah hubungan yang benar antara kuantitas P dan Q berikut berdasarkan informasi yang diberikan?
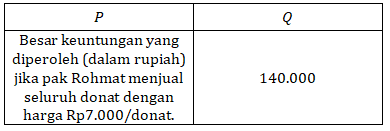
- P > Q
- Q > P
- P = Q
- Informasi yang diberikan tidak cukup untuk memutuskan salah satu dari tiga pilihan di atas.
JAWABAN : A
PEMBAHASAN :
Harga beli :
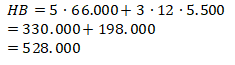
Total terdapat 5 + 3 = 8 lusin buku.
Harga jual :
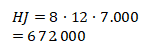
Sehingga besar keuntungan :
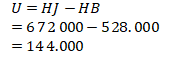
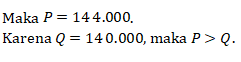

Subtopik : Aljabar
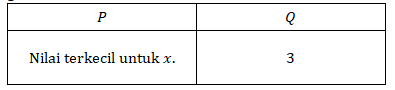
19. Diketahui ![]() dengan x adalah bilangan bulat.
dengan x adalah bilangan bulat.
Manakah hubungan yang benar antara kuantitas P dan Q berikut berdasarkan informasi yang diberikan?
- P > Q
- Q > P
- P = Q
- Informasi yang diberikan tidak cukup untuk memutuskan salah satu dari tiga pilihan di atas.
JAWABAN : A
PEMBAHASAN :
Perhatikan bahwa
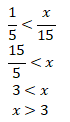
Karena x adalah bilangan bulat, maka nilai terkecil untuk x adalah 4.
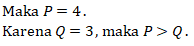

Subtopik : Bilangan, Aljabar
20. Rata-rata dari ![]() dan 21 sama dengan rata-rata dari
dan 21 sama dengan rata-rata dari ![]() 21, dan 33.
21, dan 33.
Manakah hubungan yang benar antara kuantitas P dan Q berikut berdasarkan informasi yang diberikan?

- P > Q
- Q > P
- P = Q
- Informasi yang diberikan tidak cukup untuk memutuskan salah satu dari tiga pilihan di atas.
JAWABAN : C
PEMBAHASAN :
Rata-rata dari ![]() dan 21 sama dengan rata-rata dari
dan 21 sama dengan rata-rata dari ![]() 21, dan 33, maka
21, dan 33, maka
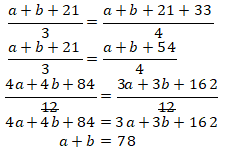
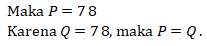

Tentu masih kurang ‘kan jika kamu hanya berlatih dari soal-soal di atas. Masih ada beberapa bulan lagi hingga waktu UTBK SBMPTN 2020. Ayo, terus berlatih lebih banyak soal lagi melalui bank soal di aplikasi Ruangguru atau memahami materi lebih dalam dengan video beranimasi dan video pembahasan soal di paket SBMPTN ruangbelajar.

















