Operasi Perkalian dan Pembagian pada Bilangan Bulat | Matematika Kelas 7

Pernah bingung nggak ketika mengalikan atau membagi bilangan bulat? Apalagi kalo angkanya negatif. Nah, di artikel Matematika kelas 7 ini, bakal dibahas sifat operasi serta contoh mudahnya biar kamu paham!

—

Kamu pasti udah nggak asing lagi kan dengan operasi penjumlahan dan pengurangan bilangan bulat. Dua operasi ini sering banget kita temui pada soal-soal matematika dasar di sekolah. Nah, ternyata selain penjumlahan dan pengurangan, ada dua operasi dasar lain yang nggak kalah penting, yaitu perkalian dan pembagian bilangan bulat.

Kenapa sih kita perlu belajar dan memahaminya? Karena operasi perkalian dan pembagian bilangan bulat sering muncul dalam kehidupan sehari-hari. Misalnya, ketika kamu ingin menghitung total harga beberapa barang yang sama, atau saat membagi rata makanan dengan teman.

Oleh karena itu, yuk, kita pelajari bersama cara menyelesaikan perkalian dan pembagian bilangan bulat! Artikel ini juga diserta sifat-sifat dan contoh soal supaya kamu semakin paham!

1. Operasi Perkalian Bilangan Bulat

Operasi ini biasanya dilambangkan dengan tanda silang (×) atau tanda titik (∙). Secara konsep, perkalian itu sebenarnya bisa dianggap sebagai bentuk penjumlahan berulang. Contohnya nih, kamu ingin menjumlahkan beberapa bilangan bulat yang sama, seperti:

Angka 3, dijumlahkan sebanyak 5 kali. Maka:

3 + 3 + 3 + 3 + 3 = 15

Nah, kamu bisa menubahnya ke dalam bentuk perkalian, menjadi:

3 × 5 = 15

Baca Juga: Penjelasan Lengkap KPK dan FPB, Apa Bedanya Ya?

Aturan Tanda dalam Operasi Perkalian Bilangan Bulat

Sebelum memahami sifat-sifat perkalian bilangan bulat, kita ingat dulu yuk, kalo:

• Bilangan bulat positif adalah bilangan yang nilainya lebih dari nol (a > 0).
• Bilangan bulat negatif adalah bilangan yang nilainya kurang dari nol (a < 0).
• Bilangan nol (0) juga termasuk bilangan bulat.

Artinya, kalo kedua bilangan punya tanda yang sama, hasilnya positif. Tapi, kalo kedua bilangan punya tanda berbeda, hasilnya negatif.

Contoh:

• 5 × 3 = 15     (positif ketemu positif, hasilnya positif)
• (–5) × (–3) = 15     (negatif ketemu negatif, hasilnya positif)
• (–5) × 3 = –15    (negatif ketemu positif, hasilnya negatif)
• 5 × (–3) = –15    (positif ketemu negatif, hasilnya negatif)

Sifat-Sifat Operasi Perkalian Bilangan Bulat

Paham sampai sini? Kita lanjut ya…

Operasi perkalian bilangan bulat itu punya sifat-sifat yang akan membantu kamu menghitung lebih cepat. Berikut sifat-sifat perkalian yang perlu kamu pahami:

1. Tertutup

Artinya, kalau kita mengalikan dua bilangan bulat, hasilnya pasti tetap berupa bilangan bulat.

Contoh: 5 × (–2) = –10 (masih bilangan bulat)

2. Identitas

Dalam perkalian, angka 1 disebut unsur netral. Kenapa? Karena setiap bilangan bulat yang dikalikan dengan 1, hasilnya akan tetap bilangan itu sendiri.

Contoh: (–7) × 1 = –7

3. Komutatif (Pertukaran)

Dalam perkalian bilangan bulat, urutan faktor tidak mempengaruhi hasil. Jadi, jika bilangan pertama dan bilangan kedua ditukar posisinya, hasilnya akan tetap sama.

Contoh: 6 × (–3) hasilnya akan sama dengan (–3) × 6, yaitu –18.

4. Asosiatif (Pengelompokan)

Kalau ada lebih dari dua bilangan bulat yang dikalikan, urutan pengelompokan bilangan juga tidak akan mempengaruhi hasil. Jadi, kamu bisa mengelompokkan bilangan dengan tanda kurung dalam urutan apapun, dan hasilnya akan tetap sama.

Contoh: (2 × –4) × 3 hasilnya akan sama dengan 2 × (–4 × 3), yaitu –24.

Baca Juga: Cara Menyelesaikan Bentuk-Bentuk Aljabar

5. Distribusi Perkalian terhadap Penjumlahan

Jadi, kalo ada bilangan bulat dikalikan dengan jumlah dari dua bilangan, kita bisa mengalikan bilangan itu ke masing-masing anggota penjumlahan, lalu menjumlahkan hasilnya.

Contoh: 2 × (3 + 5) = (2 × 3) + (2 × 5) = 6 + 10 = 14

6. Perkalian dengan Nol

Apapun bilangan bulatnya, kalau dikalikan dengan 0, hasilnya pasti 0. Sifat ini sangat mudah diingat karena berlaku untuk semua bilangan, baik bilangan positif maupun negatif.

Contoh: (–8) × 0 = 0

2. Operasi Pembagian Bilangan Bulat

Invers, atau lawan dari operasi perkalian adalah operasi pembagian. Jadi, pembagian bisa disebut sebagai “kebalikan” dari perkalian.

Operasi pembagian biasanya disimbolkan dengan tanda titik dua (÷ atau 🙂 atau tanda garis miring (/). Nah, kalau perkalian adalah penjumlahan berulang, maka pembagian bisa kita pahami sebagai pengurangan berulang sampai habis.

Contoh:

12 ÷ 3 = 4, karena 12 bisa dikurangi dengan 3 sebanyak 4 kali hingga habis, atau:

12 – 3 – 3 – 3 – 3 = 0

Syarat Operasi Pembagian Bilangan Bulat

Nah, ada satu aturan yang sangat penting dalam menyelesaikan operasi pembagian. Jika sebuah bilangan bulat a dibagi dengan bilangan bulat b, maka b tidak boleh nol (b ≠ 0).

Kenapa? Karena kalau b = 0, hasilnya akan tidak terdefinisi. Artinya, pembagian dengan nol tidak punya jawaban yang sah secara matematika.

Contoh:

10 ÷ 2 = 5

10 ÷ 0 = tidak terdefinisi nilainya

Baca Juga: Aturan Penulisan Bentuk Baku Bilangan Matematika

Aturan Tanda dalam Operasi Pembagian Bilangan Bulat

Aturannya mirip dengan perkalian, kalo kedua bilangan punya tanda yang sama, hasilnya positif. Tapi, kalo kedua bilangan punya tanda berbeda, hasilnya negatif.

Contoh:

• 12 ÷ 3 = 4    (positif ketemu positif, hasilnya positif)
• (–12) ÷ (–3) = 4    (negatif ketemu negatif, hasilnya positif)
• 12 ÷ (–3) = –4    (positif ketemu negatif, hasilnya negatif)
• (–12) ÷ 3 = –4    (negatif ketemu positif, hasilnya negatif)

Sifat-Sifat Operasi Pembagian Bilangan Bulat

Operasi pembagian juga punya aturan dan sifat yang berbeda. Supaya kamu nggak salah langkah, yuk kita bahas satu per satu sifat-sifat pembagian bilangan bulat:

1. Tidak Bersifat Komutatif

Kalau pada perkalian, kita bisa menukar posisi bilangan tanpa mengubah hasil (misalnya 3 × 4 = 4 × 3), hal itu tidak berlaku dalam pembagian. Pada pembagian, posisi bilangan sangat menentukan hasil akhirnya.

Contoh: 12 ÷ 3 = 4

Tapi, kalau dibalik, hasilnya menjadi 3 ÷ 12 = 0,25.

2. Tidak Bersifat Asosiatif

Dalam perkalian, kita juga bebas mengelompokkan bilangan tanpa mengubah hasil (misalnya (2 × 3) × 4 = 2 × (3 × 4)). Tapi dalam pembagian, cara mengelompokkan bilangan tetap mempengaruhi hasil akhir.

Contoh:

(12 ÷ 6) ÷ 2 = 2 ÷ 2 = 1.

Tetapi jika dikelompokkan, hasilnya akan berbeda, yaitu: 12 ÷ (6 ÷ 2) = 12 ÷ 3 = 4.

3. Identitas

Dalam operasi pembagian, angka 1 juga menjadi unsur identitas karena membagi bilangan berapapun dengan 1 akan menghasilkan bilangan itu sendiri.

Contoh: (–9) ÷ 1 = –9

4. Pembagian dengan Diri Sendiri, Hasilnya 1

Setiap bilangan bulat, jika dibagi dengan dirinya sendiri, hasilnya selalu 1. Namun, hati-hati! Kalau 0 ÷ 0, hasilnya tidak terdefinisi, sehingga aturan ini tidak berlaku untuk nol.

Contoh: 15 ÷ 15 = 1.

5. Hubungan dengan Perkalian

Pembagian bisa dianggap sebagai kebalikan dari perkalian. Artinya, kalau kamu tahu hasil perkalian, maka kamu bisa menemukan hasil pembagian.

Contoh: 20 ÷ 4 = 5, karena kita tahu 4 × 5 = 20.

Dengan kata lain, pembagian adalah cara mencari bilangan yang dikalikan untuk mendapatkan hasil tertentu.

Baca Juga: Mengenal Bilangan Rasional dan Irasional

Contoh Soal dan Pembahasan

1. Harga 1 kodi kain adalah Rp300.000, berapa harga 5 helai kain yang sama?

1. Rp60.000
2. Rp65.000
3. Rp70.000
4. Rp75.000

Jawaban: D

Pembahasan:

Untuk menjawab soal di atas, pertama-tama, kita cari tau dulu harga satu helai kainnya.

1 kodi kain = 20 helai kain

Maka, harga 1 helai kain = Rp 300.000 ÷ 20 = Rp15.000,00

Harga 5 helai kain = Harga 1 helai kain × 5

Harga 5 helai kain = Rp15.000 × 5

Harga 5 helai kain = Rp75.000

Jadi, harga 5 helai kain adalah Rp75.000. Jawaban yang tepat yaitu D.

2. Seorang pemborong dapat menyelesaikan bangunan pos keamanan selama 20 hari dengan total pekerja sebanyak 9 orang. Agar pekerjaan itu selesai dalam waktu 15 hari, berapa tambahan pekerja yang dibutuhkan?

1. 12 orang
2. 6 orang
3. 5 orang
4. 3 orang

Jawaban: D

Pembahasan:

Diketahui:

• Jumlah pekerja awal = 9 orang
• Lama kerja awal = 20 hari
• Lama kerja baru = 15 hari
• Jumlah pekerja baru = ?

Nah, kalo kamu menemukan tipe soal ini, kamu dapat menyelesaikannya menggunakan konsep perbandingan. Kamu juga perlu paham bahwa, ‘jika jumlah hari diperkecil, maka jumlah pekerja harus diperbesar, begitu juga sebaliknya’.

Sehingga,

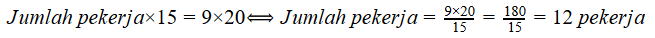
Jadi, tambahan pekerja yang diperlukan adalah 12 – 9 = 3 orang. Jawaban yang tepat yakni D.

—

Itulah pembahasan mengenai operasi perkalian dan pembagian bilangan bulat. Bagaimana? Apakah menurutmu pembahasan di atas sudah jelas?

Kalo kamu masih ingin belajar lebih banyak lagi? Boleh banget! Yuk, cobain download dan belajar bareng Master Teacher di ruangbelajar! Ada fitur konsep kilat yang bisa membantu kamu mempelajari ringkasan, dan juga video Adapto yang bisa menyesuaikan kemampuanmu menerima materi! Ayo, gabung belajar di ruangbelajar, yuk!

Referensi:

As’ari A.R, Tohir M, Valentino E, Imron Z, Taufiq I. (2017) Matematika SMP/MTs Kelas VII Semester I. Pusat Kurikulum dan Perbukuan, Balitbang, Kemendikbud.