Mengenal Bilangan Rasional & Irasional | Matematika Kelas 7

Pada artikel Matematika kelas 7 kali ini, kamu akan mengetahui apa itu bilangan rasional dan irasional, disertai contohnya. Yuk, pelajari bersama!

—

Tentunya kamu sudah belajar tentang jenis-jenis bilangan Matematika sewaktu duduk di bangku sekolah dasar bukan? Hayo, siapa di antara kamu yang masih ingat apa saja jenis-jenis bilangan Matematika itu?

Yup, benar! Ada bilangan bulat, bilangan cacah, bilangan asli, dan bilangan pecahan. Ternyata, bilangan Matematika itu banyak macamnya, lho! Tidak hanya yang kamu pelajari di sekolah dasar saja, tapi ada juga yang namanya bilangan rasional dan bilangan irasional.

Hmm, kira-kira apa ya bilangan rasional dan bilangan irasional itu? Seperti apa sih contohnya? Penasaran, kan? Kalau begitu, langsung saja yuk kita simak penjelasannya pada artikel di bawah ini!

Apa itu Bilangan Rasional?

Bilangan rasional adalah bilangan yang dapat diubah menjadi pecahan biasa (a/b) dan apabila bilangan ini diubah ke pecahan desimal, maka angkanya akan berhenti di suatu bilangan tertentu. Apabila tidak berhenti, maka akan membentuk pola pengulangan.

Contoh bilangan rasional:

Apa itu Bilangan Irasional?

Berbeda dengan bilangan rasional, kalau bilangan irasional adalah bilangan yang tidak dapat diubah ke pecahan biasa dan apabila bilangan ini diubah ke pecahan desimal, maka angkanya tidak akan berhenti dan tidak memiliki pola tertentu.

Contoh bilangan irasional:

Baca Juga: Operasi Perkalian dan Pembagian pada Bilangan Bulat

Letak Bilangan Rasional dan Irasional pada Garis Bilangan

Agar lebih jelas, coba bayangkan sebuah garis bilangan yang memuat angka-angka di sisi kiri (negatif) dan kanan (positif), dengan nol (0) di tengah.

Contoh garis bilangan. (Sumber: roboguru.com)

Bilangan rasional mudah sekali ditempatkan pada garis bilangan karena bisa ditulis dalam bentuk pecahan atau desimal yang pasti. Misalnya:

• ½ terletak di tengah antara 0 dan 1.
• –¾ ada di antara –1 dan 0, lebih dekat ke –1.
• 2 dan 0 sudah jelas posisinya di angka bulat.
• 3,25 berada sedikit setelah angka 3.

Nah, bilangan irasional juga ada di garis bilangan, hanya saja posisinya tidak bisa ditentukan secara tepat dengan pecahan sederhana. Misalnya:

• √2 ≈ 1,414, artinya posisinya ada di antara 1,4 dan 1,5.
• π ≈ 3,14159…, posisinya ada sedikit lewat angka 3, sebelum mencapai 3,2.

Jadi, meskipun bilangan irasional tidak bisa dituliskan sebagai pecahan sederhana, bilangan ini tetap bisa “didekati” dan ditempatkan di garis bilangan.

Contoh Soal dan Pembahasan

Bagaimana, paham ya sampai di sini? Nah, setelah kamu tahu apa itu bilangan rasional dan bilangan irasional, selanjutnya ayo kita latihan soal, ya. Nanti, jawabannya kita selesaikan bersama-sama. Oke?

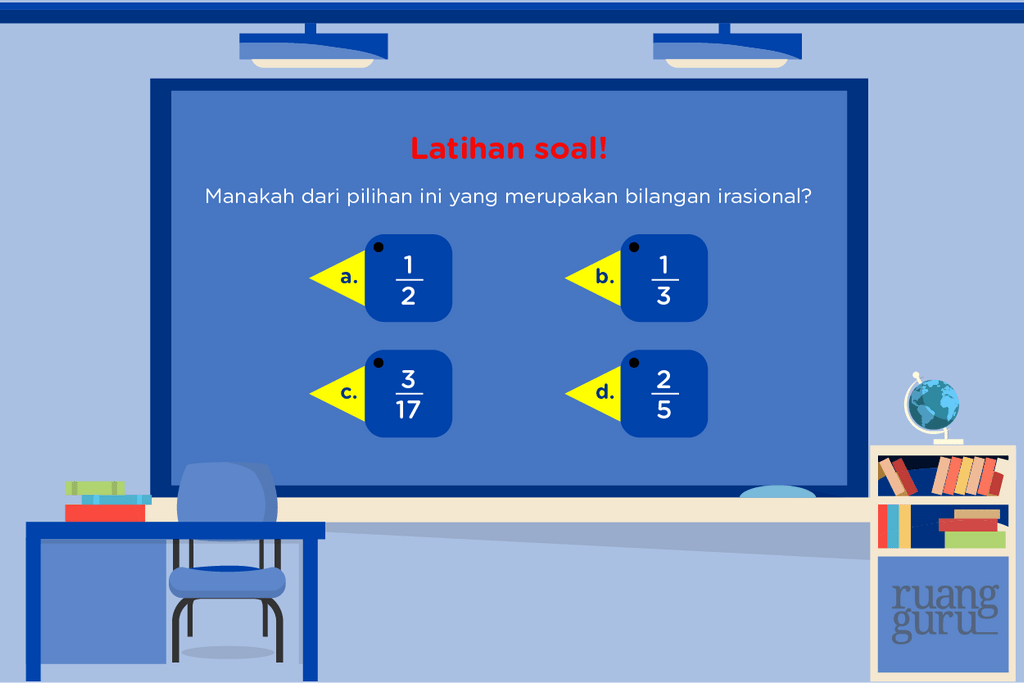
Penyelesaian:

Dalam menyelesaikan soal di atas, kita dapat menyaring setiap pilihan jawabannya. Dapat dipastikan bahwa bilangan irasional merupakan bilangan yang tidak dapat diubah ke bentuk pecahan biasa. Sehingga, opsi b dan d bukan merupakan jawabannya.

Kemudian, tersisa opsi a dan c. Ternyata, opsi a juga bukan merupakan jawaban yang tepat karena akar dari 25 merupakan bilangan bulat, yaitu 5. Jadi, sudah pasti jawabannya itu c ya, karena hasil dari √2 adalah 1,4142135623… yang angkanya tidak berhenti di suatu bilangan tertentu dan tidak berpola.

Baca Juga: Cara Menentukan Nilai Tempat Bilangan Bulat & Bilangan Desimal

—

Wah, ternyata mudah ya untuk menentukan bilangan-bilangan yang tergolong jenis bilangan rasional dan bilangan irasional. Biasanya, untuk menuliskan bilangan irasional diperlukan pembulatan angka. Misalnya, 2 atau 3 angka di belakang koma, seperti π yang dibulatkan menjadi 3,14.

Nah, bagi kamu yang ingin tahu lebih lanjut tentang materi ini, yuk, cobain download dan belajar bareng Master Teacher di ruangbelajar! Ada fitur konsep kilat yang bisa membantu kamu mempelajari ringkasan, dan juga video Adapto yang bisa menyesuaikan kemampuanmu menerima materi! Ayo, gabung belajar di ruangbelajar!

Referensi:

As’ari A.R, Tohir M, Valentino E, Imron Z, Taufiq I. (2017) Matematika SMP/MTs Kelas VII Semester I. Pusat Kurikulum dan Perbukuan, Balitbang, Kemendikbud.